REPORT: WHITE PHOSPHORUS
Technical Annex
Parametric Modelling
Projectile modelling of the flight path of the wedges was modeled using parametric software as outlined below. Items v, vi, and vii outline projectile motion functions while viii and ix outline randomization functions used for modelling wedge dispersion.
v.
Variables used in the definition. Alpha, beta, gamma and height of burst (A, B, C, and D, respectively) are determined by footage analysis. The explosion point represents a point drawn on the ground plane (E). Initial velocity (F) comes from US Army field manuals. The mass of each felt wedge is plugged in (G). Air density (H) assumes temperature between 20 and 30 degrees Celsius while the drag coefficent (I) is based on that of a flat plate. Sillhouette area (J) of each felt wedge is also included.
vii.
The distance traveled (d) of a projectile over a given period of time (dt) is dependent on its:
launch angle (A)
initial velocity (V)
Initial velocity is split into its vertical and horizontal components (Vx,Vz) based on the launch angle. Each is calculated independently:
Vx = V * cos(A)
Vz = V * sin(A)
The distance traveled (dx,dy) over a given interval of time (dt) is based its velocity (Vx,Vz) and its acceleration (Ax,Az). Each direction is calculated independently:
d x = Vx * dt +0.5 * Ax * dt
d z = Vz * dt +0.5 * Az * dt2
For a realistic path we must take into account air resistance. Acceleration due to air resistance at any time is dependent on velocity (V), drag (D), and mass (m).Component velocity is incorporated to correct for current angle:
Ax = -(D/m) * V * Vx
Az = -g - V * Vz
Drag is pre-calculated using the density of the medium through which the projectile is traveling (p), the object's coefficient of drag (C), and the silhouette area (A) of the projectile:
D = (p * C * A) / 2
Because the velocity of the projectile is continuously affected by external forces, at each instant in time it has a slightly modified velocity and therefore acceleration.
For this reason, the projectile's path must be iteratively calculated with sufficiently short time steps, or intervals updating acceleration, velocity, and position. For an accurate projectile path, and because many calculations must be performed to produce the new input variables for each time interval, a computer script was written in order to loop through the large number of calculations necessary.
viii.
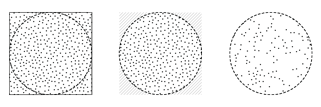
Left to right: After taking a slice through an idealized cone at one meter from the the point of burst, a square is circumscribed around the filter and then populated with 450 randomly placed points; all points that are not located within the filter are removed; the remaining points are randomly culled until only 116 are left. A vector is drawn from the point of burst to each point, thereby defining initial direction for each wedge. Each wedge is then treated as an individual entity andpushed through the model that iteratively calculates projectile motion.
ix.
VISUAL BASIC RANDOM FUNCTION
A linear-congruential method for pseudo-random number generation21.
This method takes the form of:
xn+1 = (axn+c) (mod m)
where:
xn+1 is the new value
xn is the previous value or seed
a is a constant with the value 1140671485
c is a constant with the value 12820163
m is a constant with the value of 224
The Visual Basic Random Function produces a floating point number
between 0.0 and 1.0.